Important Topics
Divide And Conquer
This technique can be divided into the following three parts:
1) Divide: This involves dividing the problem into some sub problem.
2) Conquer: Sub problem by calling recursively until sub problem solved.
3) Combine: The Sub problem Solved so that we will get find problem solution.
HuffMan's Algorithm
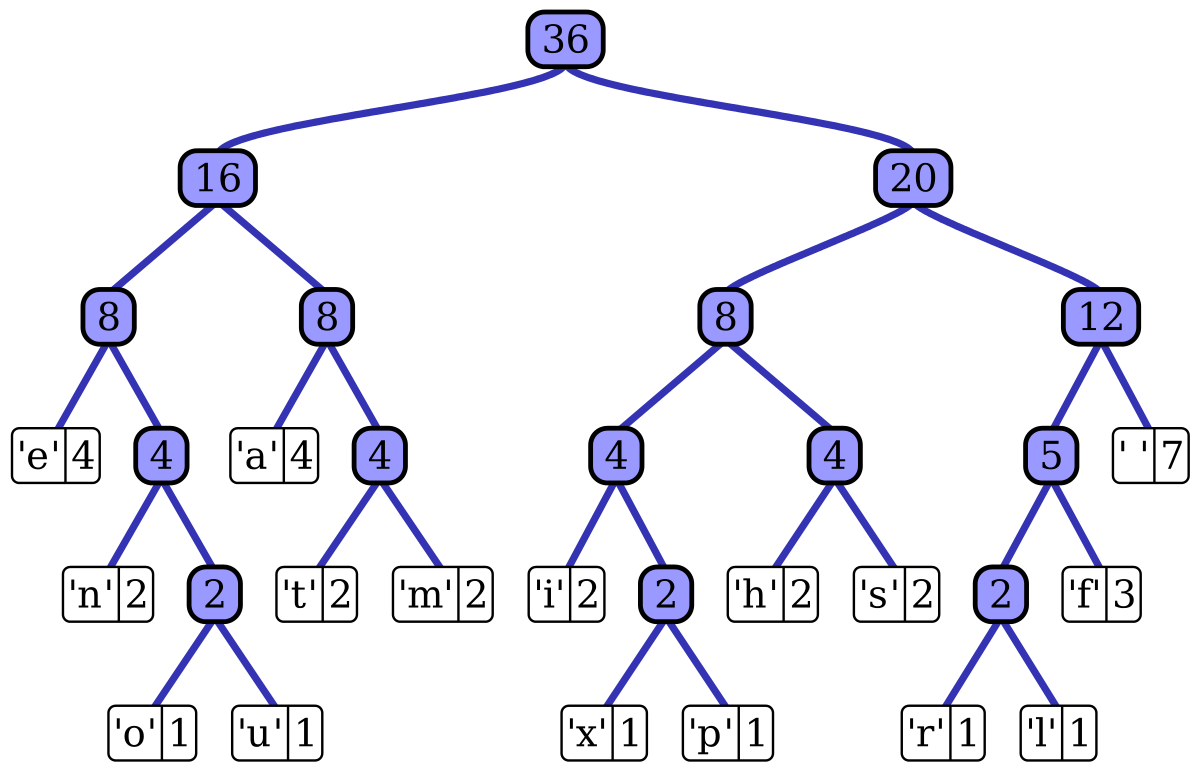
There are mainly two major parts in Huffman Coding 1) Build a Huffman Tree from input characters. 2) Traverse the Huffman Tree and assign codes to characters.
Tarvelling Salesman Problem
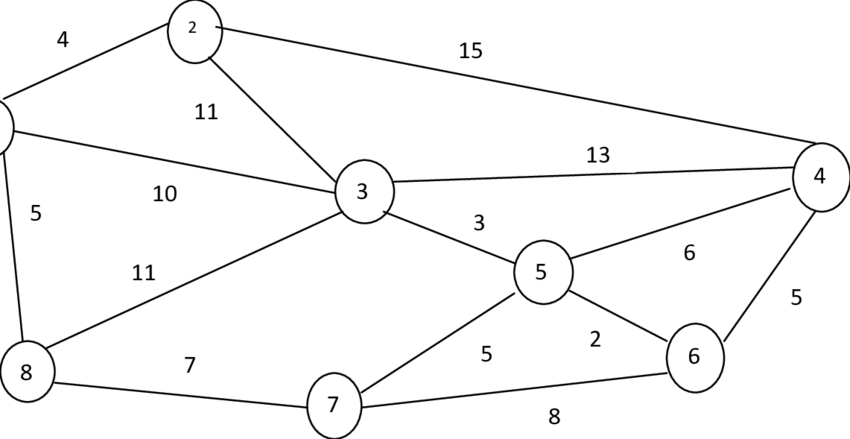
Travelling Salesman Problem (TSP): Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point
Analysis of Algorithm
The analysis of algorithms is the process of finding the computational complexity of algorithms – the amount of time, storage, or other resources needed to execute them. 1) Asyptotic Notations. 2) Worst, Average and Best Cases. 3) Solving Recurrences.
Strassen's Matrix Multiplication
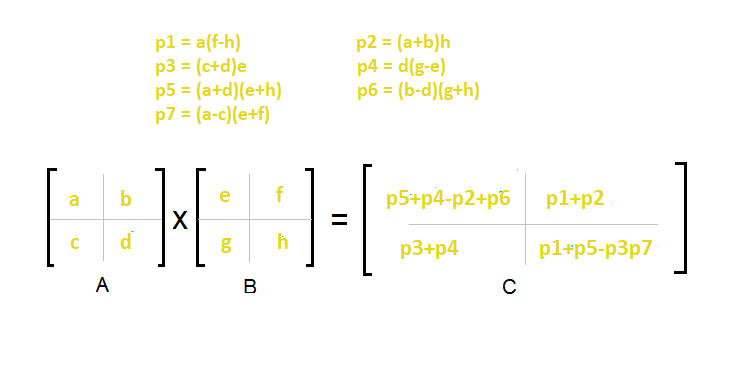
The Strassen algorithm, is an algorithm for matrix multiplication. It is faster than the standard matrix multiplication algorithm and is useful in practice for large matrices This is Based on Divide and Conquer approch
Convex Hull
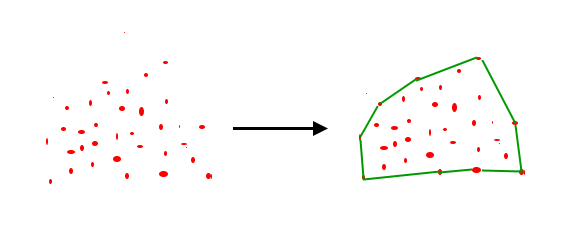
The Convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. 1) Gram Scan 2) Jarvis March.
Greedy Algorithm
Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to global solution are best fit for Greedy.
Dynamic Programming
Dynamic Programming is mainly an optimization over plain recursion. Wherever we see a recursive solution that has repeated calls for same inputs, we can optimize it using Dynamic Programming. The idea is to simply store the results of subproblems, so that we do not have to re-compute them when needed later. This simple optimization reduces time complexities from exponential to polynomial.
Kruskal's Algorithm
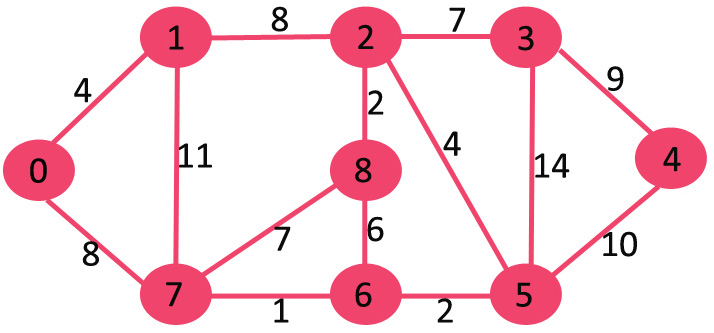
Kruskal's algorithm is a minimum-spanning-tree algorithm which finds an edge of the least possible weight that connects any two trees in the forest. It is a greedy algorithm in graph theory as it finds a minimum spanning tree for a connected weighted graph adding increasing cost arcs at each step.
Prism's Algorithm
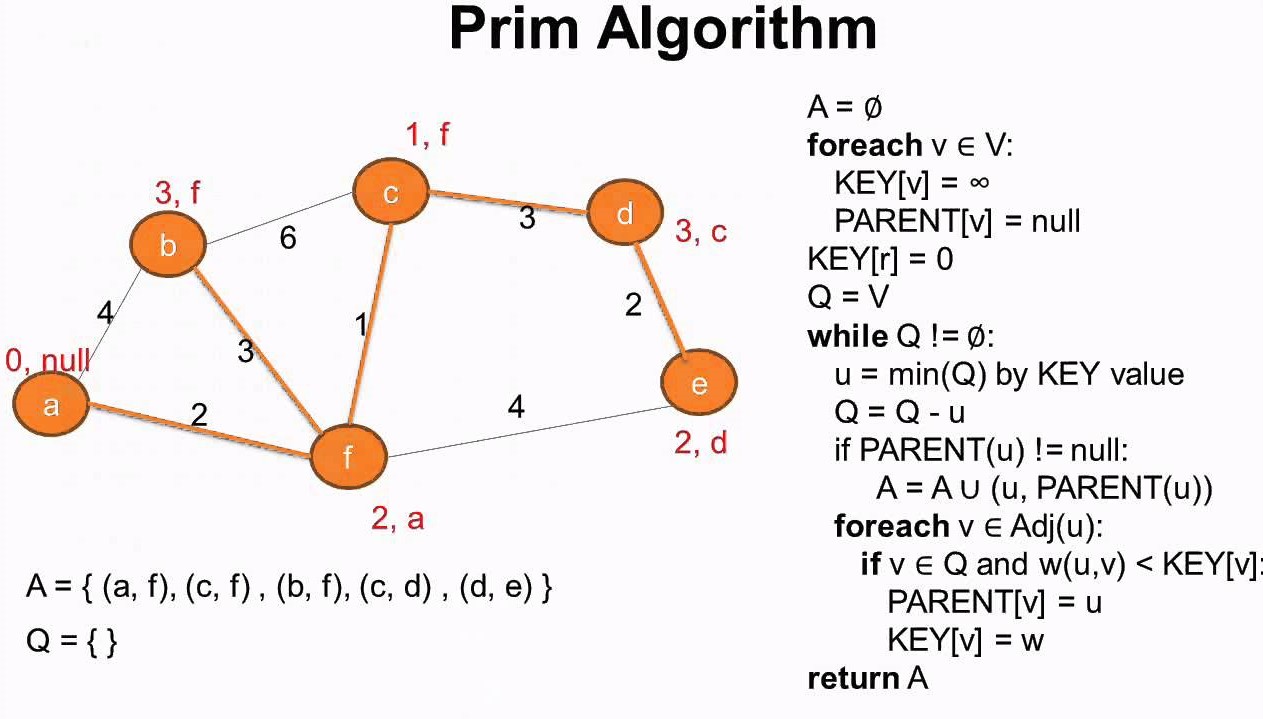
Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
Master's Thorem
The master theorem provides a solution to recurrence relations of the form
T(n)=aT(b/n)+f(n),
for constants a≥1 and b>1 with f asymptotically positive. Such recurrences occur frequently in the runtime analysis of many commonly encountered algorithms.
Randomized Algorithm
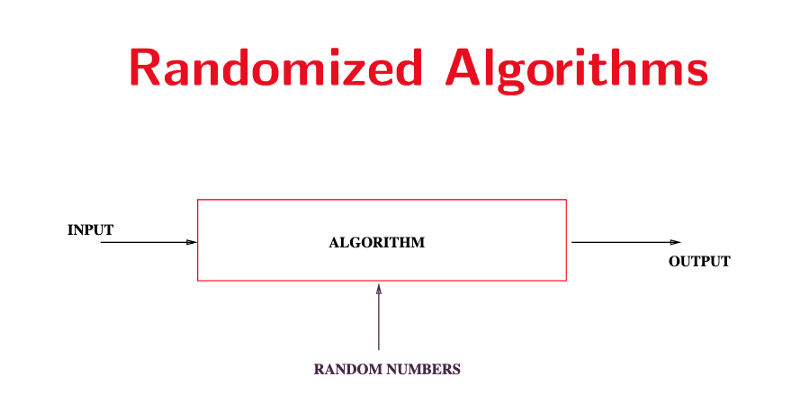
An algorithm that uses random numbers to decide what to do next anywhere in its logic is called Randomized Algorithm.
For example, in Randomized Quick Sort, we use random number to pick the next pivot
String Matching Algorithm
String-Matching Algorithms, are an important class of string algorithms that try to find a place where one or several strings (also called patterns) are found within a larger string or text.
This may significantly slow some search algorithms.
NP-Completeness
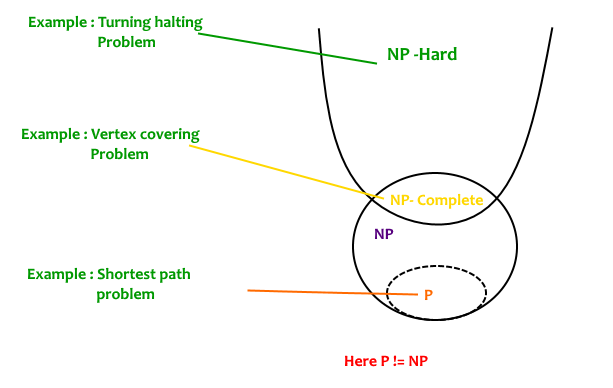
NP is set of decision problems that can be solved by a Non-deterministic Turing Machine in Polynomial time. P is subset of NP
problem that can be solved by deterministic machine in polynomial time can also be solved by non-deterministic machine in polynomial time.
N Queen Problem
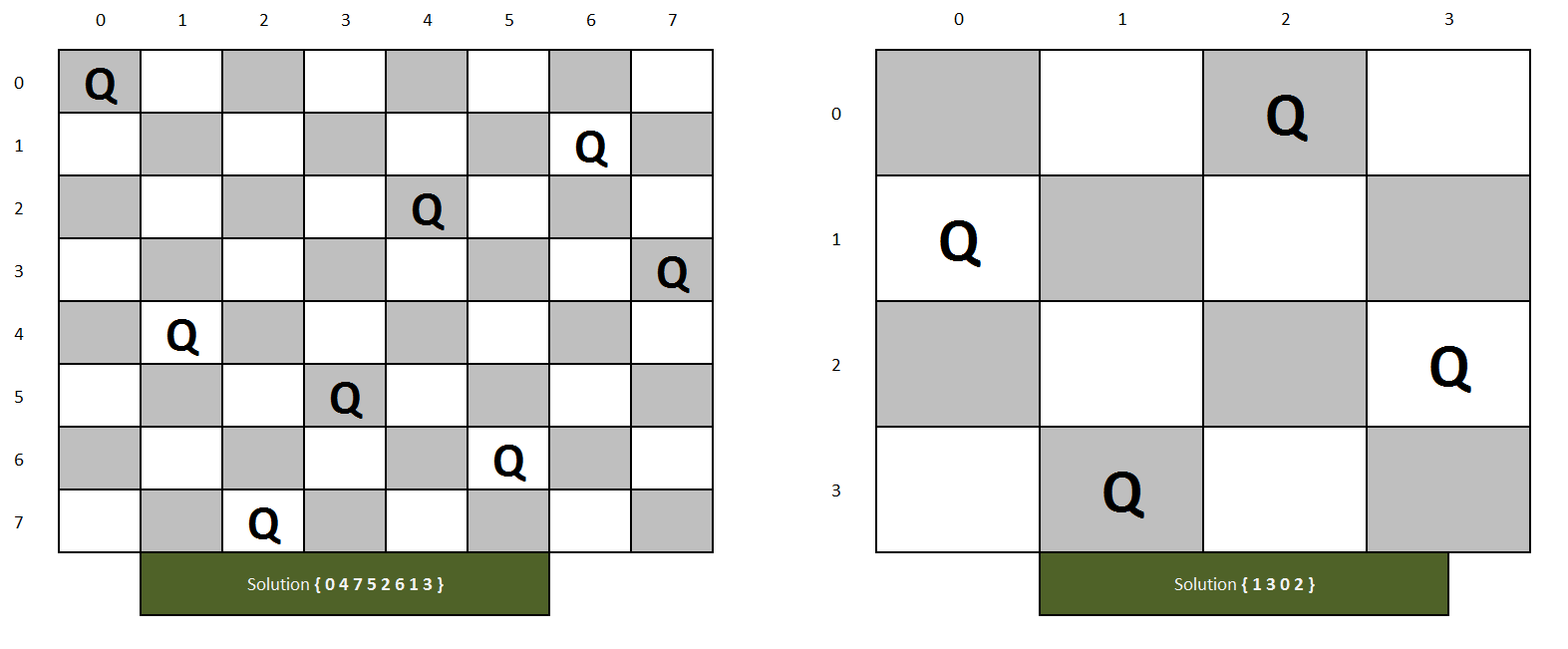
The N Queen is the problem of placing N chess queens on an NxN chessboard so that no two queens attack each other
BackTracking Algorithm
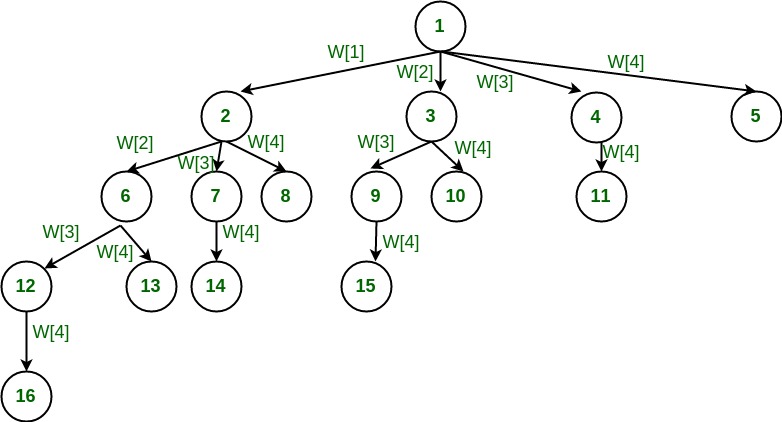
Backtracking is an algorithmic-technique for solving problems recursively by trying to build a solution incrementally, one piece at a time, removing those solutions that fail to satisfy the constraints of the problem at any point of time
by time, here, is referred to the time elapsed till reaching any level of the search tree.
Hiring Problem
Imagine an administrator who wants to hire the best secretary out of n rankable applicants for a position. The applicants are interviewed one by one in random order. A decision about each particular applicant is to be made immediately after the interview. Once rejected, an applicant cannot be recalled. During the interview, the administrator can rank the applicant among all applicants interviewed so far but is unaware of the quality of yet unseen applicants. The question is about the optimal strategy (stopping rule) to maximize the probability of selecting the best applicant.
Knapsack Problem
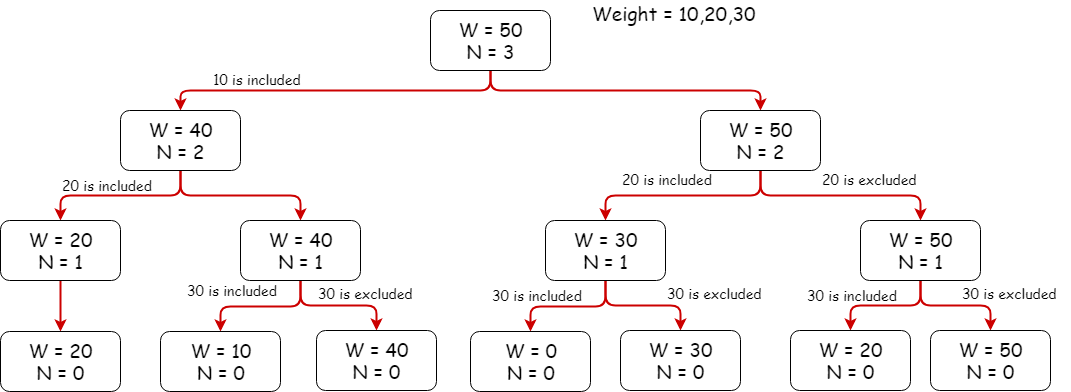
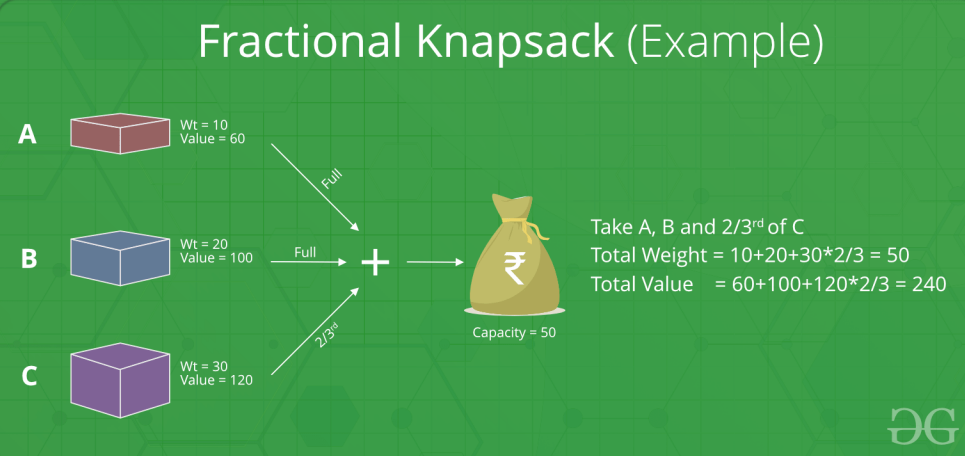
The knapsack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible.
SubSet Sum Problem
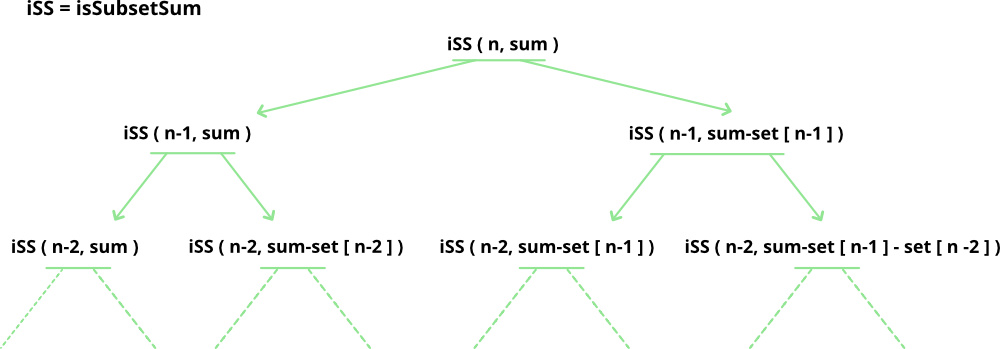
Given a set of non-negative integers, and a value sum, determine if there is a subset of the given set with sum equal to given sum.
Example:
Input: set[] = {3, 34, 4, 12, 5, 2}, sum = 9
Output: True //There is a subset (4, 5) with sum 9.
More Topics Comming Soon
I Will Upload More Interesting Topics Like This In Future
Stay Tuned
For Suggestions, message me on my Phone No. or DM me on Instagram
Phone No. and Instagram Handle is given below.